經過大約兩年前發現了的仆街悖論(請參考:http://weblog.xanga.com/hope_season/553597685/20166349032472635542.html,及對其回應之回應:http://daimones.blogspot.com/2006/12/blog-post_116563264321697382.html),今年再下一城,又發現了港女悖論。由于時間關係,今次不打算長篇累贅,上一次是把一個簡單的命題複雜化,而今次是想將一個複雜的命題簡單化。
在講港女悖論之前,先向大家介紹兩個悖論,讓大家有個理論基礎,而這兩個悖論,又與港女悖論有關,第一個是說謊者悖論,很簡單舉一個例子,就是假如我向人說:「我在說謊」,又或者我向人講了一句全稱命題:「所有的話都是假的」,則首句我在說謊這句是真話還是假話呢?如果是真話則我不是在說謊,然而我又說我在說謊,反之,如果是假話的話,則我在說謊這句似乎又是真話,這便形成一個兩難的悖論。而後一句則是所有的話都是假的,那包不包括我講這句話呢?如果包括,那就像第一個情況一樣,究竟這句話是真是假呢?羅素悖論也可以簡單點來講,如果A是一個集合,那A的元素裏包不包括A本身呢?如果A∈A,則A應該不是自身集合的元素,如果A∈A,就應是本集合的元素,即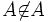 ,所以矛盾。
,所以矛盾。
不過,當然要解決說謊者悖論也不是沒辦法,如羅素自己就提出了解答,避免了自我指涉的局限,羅素提出了一個Type Theory,意即:對每一個全稱命題來說,他永遠只指涉一個type(類型),換言之,假設羅素認為全稱命題内部並不存在一邏輯矛盾,即當我說「所有的話都是假的」,則其「所有」,並不是無限制的「所有」,而是指謂那些說過的話的總和。全稱命題作為一個命題並不涉及作為一個類的本身。因為邏輯地講,我所說的那句話並不包括我這句話本身,至于這句全稱命題之為真或假,則是另一個問題。即是出現了語言層次的問題,語言層次是指對象語言(object language)和後設語言(meta language)的分別(亦有人譯作目標語言及元語言),甚至發展至之後卡普納的language order的問題,這是後話,後話不提。而另外至于前句「我正在說謊」,則克里普克或萊爾這些人會認為是非賦值的。
至于羅素悖論除了以上講的羅素類型論可以解決外,尚有ZFC系统和NBG系统及布勞威的直覺主義邏輯等。另一個簡單的做法便是重新定義集合,把所有集合都作為類,但是不是所有的類都是集合,現在把包括那種包含「所有」的類叫做本格類,不算是集合,于是就解决了,然後討論集合的時候,這類「本格類」就被取消了,當然也是一種取巧的辦法。
好,現在進入正題,有了以上的基礎後,假設有個女人聲稱:「所有女人都是港女」,那末這個女人講這句就遇上了自我指涉的問題。(其實這個問題也可以換轉做有個毒男聲稱「全世界的男人都是毒男」一樣。)
有了上述的知識,那末這個女人講的那句話並不包括她這句話本身,簡單點來說即是她可以有一個自我豁免。
那末,可能有人會以為全世界這麼多女人,這個女人如此宣稱,多她一個不多,少她一個不少,因此就算多幾個宣稱也影響不了什麼,因此這又是陷入另一個悖論,便是沙丘悖論,不過這並不是這個港女悖論的重點,因此略去不提。
但大家有沒有想過,假如所有的女人一起宣稱:「所有女人都是港女」的時候,會是怎樣?如果有自我豁免的話,那末所有女人都自我豁免的時候,那是否就所有女人都不是港女呢?如果所有女人都不是港女,那是否港女這個詞是空廢呢?如果要像定義集合那樣重新定義港女,那這港女已非彼港女了,港女的內容定義已經改變,那也就不是港女了。
因此,結論很簡單:這個世界根夲沒有港女。這個結論,就如萬曆十五年裏其中一章的標題說:「世間已無張居正」一樣震撼,因為世間已無港女了。
在講港女悖論之前,先向大家介紹兩個悖論,讓大家有個理論基礎,而這兩個悖論,又與港女悖論有關,第一個是說謊者悖論,很簡單舉一個例子,就是假如我向人說:「我在說謊」,又或者我向人講了一句全稱命題:「所有的話都是假的」,則首句我在說謊這句是真話還是假話呢?如果是真話則我不是在說謊,然而我又說我在說謊,反之,如果是假話的話,則我在說謊這句似乎又是真話,這便形成一個兩難的悖論。而後一句則是所有的話都是假的,那包不包括我講這句話呢?如果包括,那就像第一個情況一樣,究竟這句話是真是假呢?羅素悖論也可以簡單點來講,如果A是一個集合,那A的元素裏包不包括A本身呢?如果A∈A,則A應該不是自身集合的元素,如果A∈A,就應是本集合的元素,即
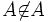 ,所以矛盾。
,所以矛盾。不過,當然要解決說謊者悖論也不是沒辦法,如羅素自己就提出了解答,避免了自我指涉的局限,羅素提出了一個Type Theory,意即:對每一個全稱命題來說,他永遠只指涉一個type(類型),換言之,假設羅素認為全稱命題内部並不存在一邏輯矛盾,即當我說「所有的話都是假的」,則其「所有」,並不是無限制的「所有」,而是指謂那些說過的話的總和。全稱命題作為一個命題並不涉及作為一個類的本身。因為邏輯地講,我所說的那句話並不包括我這句話本身,至于這句全稱命題之為真或假,則是另一個問題。即是出現了語言層次的問題,語言層次是指對象語言(object language)和後設語言(meta language)的分別(亦有人譯作目標語言及元語言),甚至發展至之後卡普納的language order的問題,這是後話,後話不提。而另外至于前句「我正在說謊」,則克里普克或萊爾這些人會認為是非賦值的。
至于羅素悖論除了以上講的羅素類型論可以解決外,尚有ZFC系统和NBG系统及布勞威的直覺主義邏輯等。另一個簡單的做法便是重新定義集合,把所有集合都作為類,但是不是所有的類都是集合,現在把包括那種包含「所有」的類叫做本格類,不算是集合,于是就解决了,然後討論集合的時候,這類「本格類」就被取消了,當然也是一種取巧的辦法。
好,現在進入正題,有了以上的基礎後,假設有個女人聲稱:「所有女人都是港女」,那末這個女人講這句就遇上了自我指涉的問題。(其實這個問題也可以換轉做有個毒男聲稱「全世界的男人都是毒男」一樣。)
有了上述的知識,那末這個女人講的那句話並不包括她這句話本身,簡單點來說即是她可以有一個自我豁免。
那末,可能有人會以為全世界這麼多女人,這個女人如此宣稱,多她一個不多,少她一個不少,因此就算多幾個宣稱也影響不了什麼,因此這又是陷入另一個悖論,便是沙丘悖論,不過這並不是這個港女悖論的重點,因此略去不提。
但大家有沒有想過,假如所有的女人一起宣稱:「所有女人都是港女」的時候,會是怎樣?如果有自我豁免的話,那末所有女人都自我豁免的時候,那是否就所有女人都不是港女呢?如果所有女人都不是港女,那是否港女這個詞是空廢呢?如果要像定義集合那樣重新定義港女,那這港女已非彼港女了,港女的內容定義已經改變,那也就不是港女了。
因此,結論很簡單:這個世界根夲沒有港女。這個結論,就如萬曆十五年裏其中一章的標題說:「世間已無張居正」一樣震撼,因為世間已無港女了。

2 留言:
當我說香港所有女生都是港女時, 當然是包括自身的。
1. 香港所有女性都是港女
2. 說的人是女性, 而且是香港人
1+2=說的人是港女。
若說當句子由自己說出來的時候, 自身便能「免役」, 那說的人本身就犯了邏輯上的錯誤。
另, 我覺得沒有豁免的必要。是港女又如何呢? 不過是個標籤而已, 在同一個社會環境下生存, 染有相類的想法或作風也是自然的事。然而, 人除了共性, 也同時有著獨立性。若只在乎其共性, 那也是人家的自由, 而且他/她所說的也不見得盡是錯, 只不過是過於簡化而已, 沒有否定或高呼「我不是這樣」的必要。
我我想回覆舒爾賽 10/20/2008的港女文章,「所有的話都是假的」是二分問題,即非黑即白問題,引用先生所引的邏輯推論去證「所有」不包括該話本身,可以理解。但「所有女人都是港女」是歸類問題,不是非黑即白的。故推論感勉強。請指教! Mark
發佈留言